II.1.2 Rotation in XY plane and algebraic notations

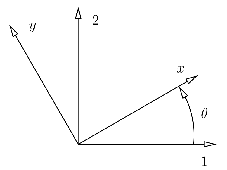
One common operation in classical laminate analysis is to rotate vectors, tensors and matrices. One summarizes here the operations one uses in the rest of this Chapter and in FeResPost. This rotation is represented in Figure II.1.3.

Figure II.1.3: Rotation of angle $\theta$ around the origin in $O_{12}$ plane.

II.1.2.0.1 Rotation of base vectors

For such a rotation, the vectors $e_x$ and $e_y$ are expressed as a function of $e_1$ and $e_2$ as:

To simplify the notations, one introduces the symbols $c=\cos <!--FUNCTION\; APPLICATION-->\theta$ and $s=\sin <!--FUNCTION\; APPLICATION-->\theta$. Also, one prefers to write the more general 3D version of the transformation:

The inverse relation corresponds to a rotation of angle $-\theta$ and is obtained by changing the signs of the sinuses in the rotation matrix:

II.1.2.0.2 Transformation of vector and tensor components

The expressions (II.1.1) and (II.1.2) can be used to transform the components of vectors. For example:

For the transformation of 2D tensors, the transformation matrix is used twice. For example, a Cauchy stress tensor is transformed as follows:

II.1.2.0.3 Matricial notations

As the Cauchy stress tensor is symmetric, expression (II.1.4) is more conveniently written in a matricial form as follows:

The same expression applies to the components of the strain tensor, which is also symmetric:

However, unfortunately, the classical laminate analysis is universally written using angular shear components for the strain tensor:

Using the angular components, the matricial expression to be used for the rotation becomes:

An interesting aspect of the transformations (II.1.5) and (II.1.6) is that one can apply the transformation separately on sub-groups of components:

• For the in-plane components, one uses the following transformations:

  $$\left(\begin{array}{c}\hfill {\sigma }_{xx}\hfill \\ \hfill {\sigma }_{yy}\hfill \\ \hfill {\tau }_{xy}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill c^2\hfill & \hfill s^2\hfill & \hfill 2cs\hfill \\ \hfill s^2\hfill & \hfill c^2\hfill & \hfill -2cs\hfill \\ \hfill -cs\hfill & \hfill cs\hfill & \hfill c^2-s^2\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill {\sigma }_{11}\hfill \\ \hfill {\sigma }_{22}\hfill \\ \hfill {\tau }_{12}\hfill \end{array}\right),$$

  (II.1.7)

  $$\left(\begin{array}{c}\hfill {ϵ}_{xx}\hfill \\ \hfill {ϵ}_{yy}\hfill \\ \hfill {\gamma }_{xy}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill c^2\hfill & \hfill s^2\hfill & \hfill cs\hfill \\ \hfill s^2\hfill & \hfill c^2\hfill & \hfill -cs\hfill \\ \hfill -2cs\hfill & \hfill 2cs\hfill & \hfill c^2-s^2\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill {ϵ}_{11}\hfill \\ \hfill {ϵ}_{22}\hfill \\ \hfill {\gamma }_{12}\hfill \end{array}\right).$$

  (II.1.8)

• For the out of plane shear, the transformation is:

  $$\left(\begin{array}{c}\hfill {\gamma }_{zx}\hfill \\ \hfill {\gamma }_{yz}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill c\hfill & \hfill s\hfill \\ \hfill -s\hfill & \hfill c\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill {\gamma }_{13}\hfill \\ \hfill {\gamma }_{23}\hfill \end{array}\right).$$

  The relation has been written for the out-of-plane shear components of strain tensor. Note however, that the relation is the same for the out-of-plane shear components of Cauchy stress tensor.

• The $zz$ or $33$ component is left unchanged.

This contributes to justify some of the simplifications of the classical laminate analysis; among others, the decoupling of in-plane and flexural deformation of the laminate on one hand from the out-of-plane shear on the other hand. The third direction is systematically neglected: ${\sigma }_{33}={ϵ}_{33}=0$. The inverse of relation (II.1.7) is obviously;

II.1.2.0.4 Introduction of a short notation

In order to simplify the notations, one introduces the following notations:

These matrices are not independent. For example:

The transformations of the components of strain tensor (II.1.8) and stress tensor (II.1.9) are then written:

Similarly, for the out-of-plane shear stresses and strains one writes the following relations: